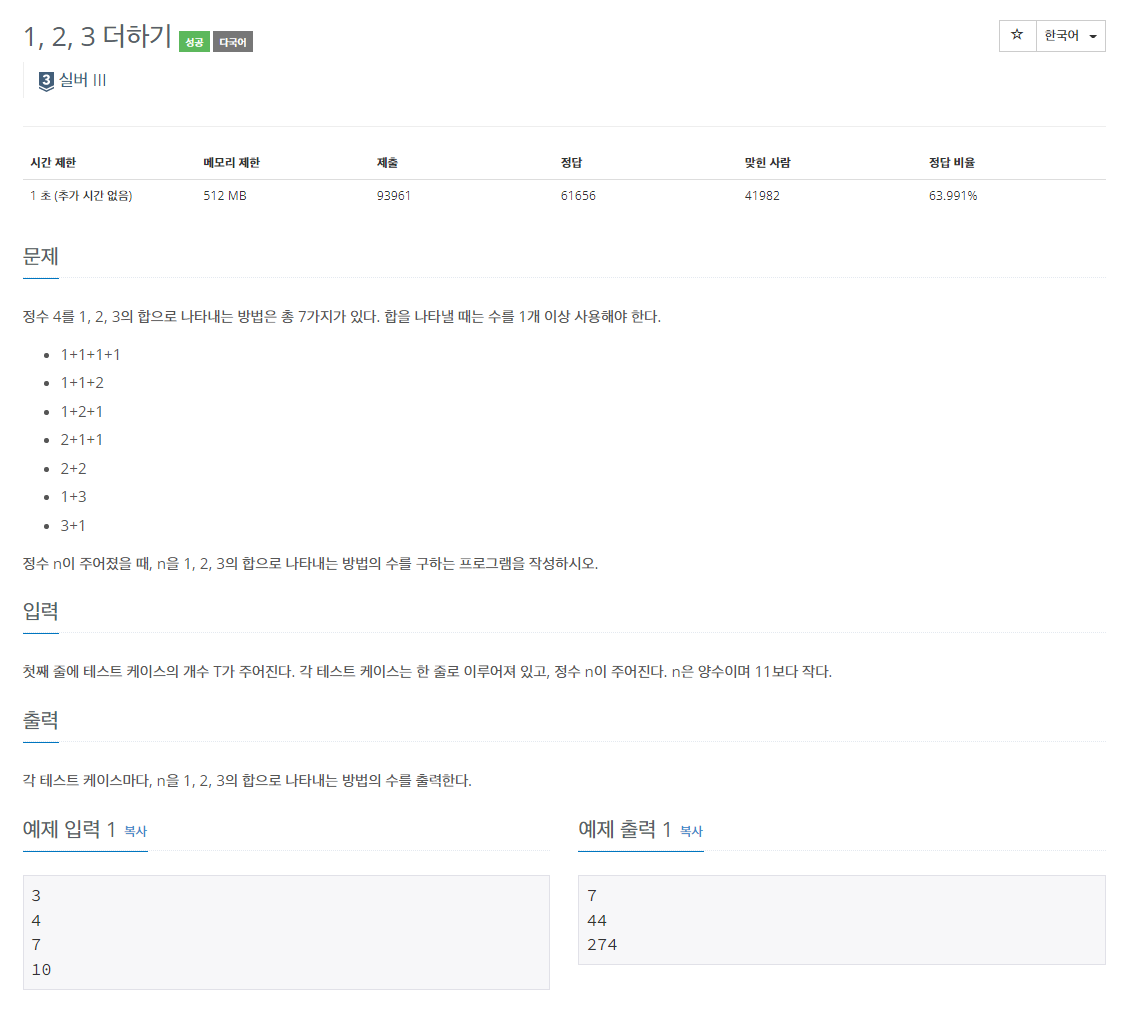
1, 2, 3 갯수를 일일히 구하는 것은 비효율적인 접근이겠습니다.
1부터 n을 하나씩 늘려가면서 n을 1, 2, 3의 합으로 나타낼 수 있는 경우들을 직접 적어보고 적절한 점화식을 찾아봅시다.
더보기
n이...
1 인 경우 - 1
2 인 경우 - 1, 1 / 2
3 인 경우 - 1, 1, 1 / 1, 2 / 2, 1 / 3
4 인 경우 - 1, 3 / 1, 1, 2 / 2, 2 / 1, 1, 1, 1 / 1, 2, 1 / 2, 1, 1 / 3, 1
위 경우들을 살펴보면,
n이 1인 방법의 뒤에 3을 붙이고, 2인 방법들의 뒤에 2를 붙이고, 3인 방법들의 뒤에 1을 붙이면
n이 4인 방법들을 완성할 수 있다는 규칙이 보입니다.
즉, A(n)이 n을 1, 2, 3의 합으로 나타낼 수 있는 경우의 수라고 가정했을 때,
A(n) = A(n - 3) + A(n - 2) + A(n - 1) 이라는 사실을 확인할 수 있습니다.
#include <iostream>
#include <queue>
using namespace std;
int main() {
cin.tie(NULL);
cout.tie(NULL);
ios_base::sync_with_stdio(false);
int t, temp;
int max = 0;
cin >> t;
int res[12];
res[1] = 1;
res[2] = 2;
res[3] = 4;
queue<int> q;
for (int i = 0; i < t; ++i) {
cin >> temp;
if (temp > max) max = temp;
q.push(temp);
}
for (int i = 4; i <= max; ++i) {
res[i] = res[i - 3] + res[i - 2] + res[i - 1];
}
while (!q.empty()) {
cout << res[q.front()] << "\n";
q.pop();
}
return 0;
}'Algorithm > 백준 C++' 카테고리의 다른 글
| 백준 3673번 :: 나눌 수 있는 부분 수열 - C++ (0) | 2023.08.07 |
|---|---|
| 백준 2580 : 스도쿠 - C++ (0) | 2023.05.11 |
| 백준 11726 : 2×n 타일링 - C++ (0) | 2023.02.05 |
| 백준 15829 : Hashing - C++ (0) | 2023.02.02 |
| 백준 26007번 : Codepowers - C++ (0) | 2023.02.01 |




댓글